El 1831, Michael Faraday va explicar la teoria de inducció electromagnètica científicament. El terme inductància és la capacitat del conductor d’oposar-se al corrent que hi circula i que indueix una emf. A partir de les lleis d’inducció de Faraday, s’indueix una força electromotriu (CEM) o tensió el conductor a causa del canvi del camp magnètic a través del circuit. Aquest procés s’indica com a inducció electromagnètica. La tensió induïda s’oposa a la velocitat de canvi de corrent. Es coneix com a llei de Lenz i el voltatge induït es torna a anomenar CEM. La inductància es divideix en dos tipus. Són, l’autoinductància i la inductància mútua. Aquest article tracta sobre la inductància mútua de dues bobines o conductors.
Què és la inductància mútua?
Definició: La inductància mútua de dues bobines es defineix com l’emf induïda a causa del camp magnètic d’una bobina s’oposa al canvi de corrent i tensió en una altra bobina. Això significa que les dues bobines estan unides magnèticament a causa del canvi de magnètic flux. El camp magnètic o flux d'una bobina enllaça amb una altra bobina. Això es denota per M.
El corrent que flueix en una bobina indueix el voltatge en una altra bobina a causa del canvi de flux magnètic. La quantitat de flux magnètic relacionat amb les dues bobines és directament proporcional a la inductància mútua i al canvi de corrent.
Teoria de la inductància mútua
La seva teoria és molt senzilla i es pot entendre utilitzant dues o més bobines. Va ser descrit per un científic nord-americà Joseph Henry al segle XVIII. Es coneix com una de les propietats de la bobina o conductor que s’utilitza al circuit. La propietat inductància és a dir, si el corrent d’una bobina canvia amb el temps, l’EMF induirà a una altra bobina.
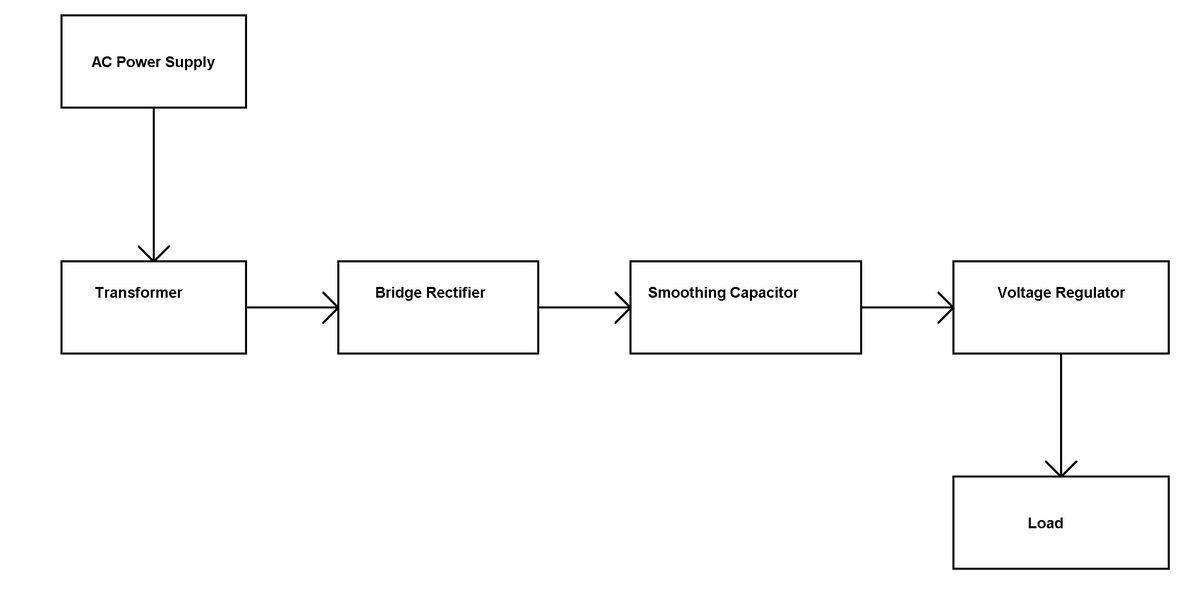
Oliver Heaviside va introduir el terme inductància l'any 1886. La propietat de la inductància mútua és el principi de treball de molts components elèctrics que funcionen amb el camp magnètic. Per exemple, el transformador és un exemple bàsic d’inductància mútua.
El principal inconvenient de la inductància mútua és que la fuga de la inductància d’una bobina pot interrompre el funcionament d’una altra bobina mitjançant la inducció electromagnètica. Per reduir les fuites, cal un control elèctric
El posicionament de dues bobines al circuit decideix la quantitat d’inductància mútua que enllaça amb una a l’altra bobina.
Fórmula d’inductància mútua
La fórmula de dues bobines es dóna com
M = (μ0.μr. N1. N2. A) / L
On μ0 = permeabilitat de l'espai lliure = 4π10-2
μ = permeabilitat del nucli de ferro tou
N1 = voltes de la bobina 1
N2 = voltes de la bobina 2
A = àrea de la secció transversal en m2
L = longitud de la bobina en metres
Unitat d’inductància mútua
La unitat d’inductància mútua és el kg. m2.s-2.A-2
La quantitat d’inductància produeix la tensió d’un volt a causa de la velocitat de canvi de corrent d’1A / segon.
El Unitat SI d’inductància mútua és Henry. Es pren del científic nord-americà Joseph Henry, que va explicar el fenomen de dues bobines.
La dimensió de la inductància mútua
Quan dues o més bobines s’uneixen magnèticament amb el mateix flux magnètic, la tensió induïda en una bobina és proporcional a la velocitat de canvi de corrent d’una altra bobina. Aquest fenomen es coneix com inductància mútua.
Considereu que la inductància total entre les dues bobines és L ja que M = √ (L1L2) = L
La dimensió d'aquesta es pot definir com la proporció de la diferència de potencial amb la taxa de canvi de corrent. Es dóna com
Com que M = √L1L2 = L
L = € / (dI / dt)
On € = CEM induït = treball realitzat / càrrega elèctrica respecte al temps = M. L2. T-2/ IT = M.L2.T-3. Jo-1o € = M. L-2. T-3. A-1(Des que I = A)
Per inductància,
ϕ = LI
L = ϕ / A = (B. L2) / A
On B = camp magnètic = (MLT-2) / LT-1AT = MT-2A-1
Flux magnètic ϕ = BL2= MT-2L2A-1
el valor substitutiu de B i ϕ està per sobre de la fórmula L
L = MT-2L2.A-2
Es dóna la dimensió de la inductància mútua quan L1 i L2 són iguals que
M = L / (T-2L2.A-2)
M = LT2L2.A-2
Derivació
Seguiu el procés per obtenir el derivació d’inductància mútua .
La proporció de CEM induïda en una bobina i la taxa de canvi de corrent en una altra bobina és inductància mútua.
Considereu les dues bobines L1 i L2 com es mostra a la figura següent.

Dues bobines
Quan el corrent a L1 canvia amb el temps, el camp magnètic també canvia amb el temps i canvia el flux magnètic relacionat amb la segona bobina L2. A causa d’aquest canvi de flux magnètic, s’indueix un CEM a la primera bobina L1.
A més, la taxa de canvi de corrent a la primera bobina indueix CEM a la segona bobina. Per tant, la CEM s’indueix a les dues bobines L1 i L2.
Això es dóna com
€ = M (dI1 / dt)
M = € / (dI1 / dt). … .. Equació 1
Si € = 1 volt i dI1 / dt = 1Amp, llavors
M = 1 Henry
A més,
La velocitat de canvi de corrent en una bobina produeix el flux magnètic en la primera bobina i s’associa amb la segona bobina. A continuació, a partir de les lleis de Faraday sobre la inducció electromagnètica (la tensió induïda és directament proporcional a la velocitat de canvi del flux magnètic lligat) a la segona bobina, la CEM induïda es dóna com
€ = M / (dI1 / dt) = d (MI1) / dt ... .. Equació 2
€ = N2 (dϕ12 / dt) = d (N2ϕ12) / dt ... eq 3
Igualant l’equació 2 i 3
MI1 = N2ϕ12
M = (N2ϕ12) / I1 Henry
On M = inductància mútua
€ = inductància mútua CEM
N2 = no de girs a la primera bobina L1
I1 = corrent a la primera bobina
ϕ12 = flux magnètic unit en dues bobines.
La inductància mútua entre les dues bobines depèn del nombre de girs de la segona bobina o de la bobina adjacent i de l'àrea de la secció transversal
Distància entre dues bobines.
La CEM induïda a la primera bobina a causa de la velocitat de canvi de flux es dóna com,
E = -M12 (dI1 / dt)
El signe menys indica oposició a la velocitat de canvi de corrent a la primera bobina quan s’indueix el CEM.
Inductància mútua de dues bobines
La inductància mútua de dues bobines es pot augmentar col·locant-les sobre un nucli de ferro tou o augmentant el nombre de voltes de les dues bobines. Existeix un acoblament unitari entre les dues bobines quan estan enrotllades estretament sobre un nucli de ferro tou. La fuita de flux seria petita.
Si la distància entre les dues bobines és curta, el flux magnètic produït a la primera bobina interactua amb totes les voltes de la segona bobina, la qual cosa resulta en grans EMF i inductància mútua.

Inductància mútua de dues bobines
Si les dues bobines estan més allunyades i separades les unes de les altres en angles diferents, el flux magnètic induït a la primera bobina genera una EMF feble o petita a la segona bobina. Per tant, la inductància mútua també serà petita.

Dues bobines de distància
Per tant, el valor d'això depèn principalment del posicionament i l'espaiat de dues bobines sobre un nucli de ferro tou. Penseu en la figura, que mostra que les dues bobines estan ben enrotllades una a la part superior del nucli de ferro tou.

Les bobines estan estretament ferides
El canvi de corrent a la primera bobina produeix un camp magnètic i fa passar les línies magnètiques per la segona bobina, que s’utilitza per calcular la inductància mútua.
La inductància mútua de dues bobines es dóna com
M12 = (N2ϕ12) / I1
M21 = (N1ϕ21) / I2
On M12 = inductància mútua de la primera bobina a la segona bobina
M21 = inductància mútua de la segona bobina a la bobina de puny
N2 = voltes de la segona bobina
N1 = voltes de la primera bobina
I1 = corrent que flueix al voltant de la primera bobina
I2 = corrent que flueix al voltant de la segona bobina.
Si el flux relacionat amb el L1 i el L2 és el mateix que el corrent que circula al seu voltant, la inductància mútua de la primera bobina a la segona bobina es dóna com a M21
La inductància mútua de dues bobines es pot definir com M12 = M21 = M
Per tant, dues bobines depenen principalment de la mida, els girs, la posició i l’espaiat entre les dues bobines.
L’autoinductància de la primera bobina és
L1 = (μ0.μr.N12.A) / L
L’autoinductància de les segones bobines és
L2 = (μ0.μr.N2.A) / L
Multiplicar creuadament les dues fórmules anteriors
Llavors la inductància mútua de dues bobines, que existeix entre elles, es dóna com a
M2= L1. L2
M = √ (L1.L2) Henry
L'equació anterior dóna un flux magnètic = 0
Acoblament 100% magnètic entre L1 i L2
Coeficient d'acoblament
La fracció de flux magnètic lligada amb les dues bobines al flux magnètic total entre les bobines es coneix com a coeficient d’acoblament i es denota per ‘k’. El coeficient d’acoblament es defineix com la proporció del circuit obert a la relació de tensió real i la relació de flux magnètic obtinguda a les dues bobines. Atès que el flux magnètic d’una bobina s’enllaça amb una altra bobina.
El coeficient d’acoblament especifica la inductància d’un inductor. Si l’acoblament del coeficient k = 1, les dues bobines s’acoblen fortament. Per tant, totes les línies de flux magnètic d’una bobina tallen totes les voltes d’una altra bobina. Per tant, la inductància mútua és la mitjana geomètrica de les inductàncies individuals de dues bobines.
Si les inductàncies de dues bobines són les mateixes (L1 = L2), la inductància mútua entre les dues bobines és igual a la inductància d’una sola bobina. Això significa,
M= √(L1 . L2) = L
on L = inductància d’una sola bobina.
Factor d'acoblament entre bobines
El factor d'acoblament entre bobines es pot representar com a 0 i 1
Si el factor d'acoblament és 1, no hi ha cap acoblament inductiu entre les bobines.
Si el factor d’acoblament és 0, hi ha un acoblament inductiu màxim o complet entre les bobines.
L’acoblament inductiu es representa en 0 i 1, però no en percentatges.
Per exemple, si k = 1, les dues bobines s’acoblen perfectament
Si k> 0,5, les dues bobines s’acoblen fortament
Si k<0.5, then the two coils are coupled loosely.
Per trobar el factor d'acoblament del coeficient entre les dues bobines, s'ha d'aplicar la següent equació,
K = M / √ (L1. L2)
M = k. √ (L1. L2)
On L1 = inductància de la primera bobina
L2 = inductància de la segona bobina
M = inductància mútua
K = factor d'acoblament
Aplicacions
El aplicacions d’inductància mútua són,
- Transformador
- Motors elèctrics
- Generadors
- Altres dispositius elèctrics que funcionen amb un camp magnètic.
- S'utilitza en el càlcul de corrents de Foucault
- Processament de senyals digitals
Per tant, això es tracta una visió general de la inductància mútua - definició, fórmula, unitat, derivació, factor d'acoblament, acoblament de coeficients i aplicacions. Aquí teniu una pregunta: Quin és l’inconvenient de la inductància mútua entre dues bobines?